Next Topic

字典树(trie)

数据结构与算法第四章树(tree) 字典树(trie)

一、字典树的概念

字典树，顾名思义，是关于“字典”的一棵树。即：它是对于字典的一种存储方式（所以是一种数据结构而不是算法）。这个词典中的每个“单词”就是从根节点出发一直到某一个目标节点的路径，路径中每条边的字母连起来就是一个单词。

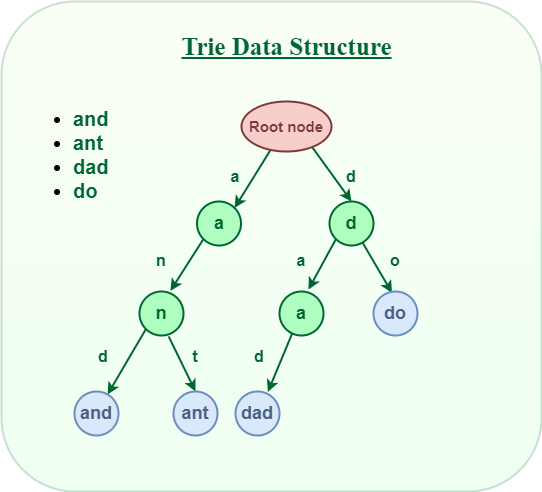
二、字典树的功能

根据字典树的概念，我们可以发现：字典树的本质是把很多字符串拆成单个字符的形式，以树的方式存储起来。所以我们说字典树维护的是”字典“。那么根据这个最基本的性质，我们可以由此延伸出字典树的很多妙用。简单总结起来大体如下：

1、维护字符串集合（即字典）。
2、向字符串集合中插入字符串（即建树）。
3、查询字符串集合中是否有某个字符串（即查询）。
4、统计字符串在集合中出现的个数（即统计）。
5、将字符串集合按字典序排序（即字典序排序）。
6、求集合内两个字符串的LCP（Longest Common Prefix，最长公共前缀）（即求最长公共前缀）。

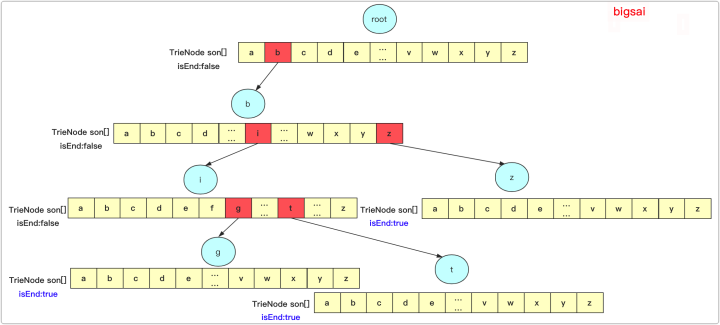
三、字典树的代码实现

#include <iostream>
using namespace std;

const int ALPHABET_SIZE = 26; // 字母表大小为26个英文字母

// Trie树节点结构
struct TrieNode {
    struct TrieNode* children[ALPHABET_SIZE]; // 子节点数组，每个节点有26个子节点
    bool isEndOfWord; // 标记是否为单词结束
};

// 返回初始化为NULL的新Trie节点
struct TrieNode* getNode(void){
    struct TrieNode* pNode = new TrieNode;
    pNode->isEndOfWord = false; // 初始化为非单词结束
    for (int i = 0; i < ALPHABET_SIZE; i++)
        pNode->children[i] = NULL; // 初始化所有子节点为NULL
    return pNode;
}

// 如果不存在则将键插入Trie树，如果键是Trie树节点的前缀，则仅标记叶节点
void insert(struct TrieNode* root, string key){
    struct TrieNode* pCrawl = root;
    for (int i = 0; i < key.length(); i++) {
        int index = key[i] - 'a'; // 计算字母在字母表中的索引
        if (!pCrawl->children[index])
            pCrawl->children[index] = getNode(); // 如果对应子节点不存在则创建新节点
        pCrawl = pCrawl->children[index]; // 移动到子节点
    }
    // 标记最后一个节点为单词结束
    pCrawl->isEndOfWord = true;
}

// 如果键在Trie树中存在则返回true，否则返回false
bool search(struct TrieNode* root, string key){
    struct TrieNode* pCrawl = root;
    for (int i = 0; i < key.length(); i++) {
        int index = key[i] - 'a'; // 计算字母在字母表中的索引
        if (!pCrawl->children[index])
            return false; // 如果对应子节点不存在则返回false
        pCrawl = pCrawl->children[index]; // 移动到子节点
    }
    // 返回当前节点是否为单词结束
    return (pCrawl != NULL && pCrawl->isEndOfWord);
}

// 如果根节点没有子节点则返回true，否则返回false
bool isEmpty(TrieNode* root){
    for (int i = 0; i < ALPHABET_SIZE; i++)
        if (root->children[i]) return false; // 如果有子节点则返回false
    return true; // 没有子节点则返回true
}

// 递归函数从给定的Trie树中删除一个键
TrieNode* remove(TrieNode* root, string key, int depth = 0){
    // 如果树为空
    if (!root)
        return NULL;

    // 如果正在处理键的最后一个字符
    if (depth == key.size()) {
        // 删除给定键后该节点不再是单词结束
        if (root->isEndOfWord)
            root->isEndOfWord = false;
        // 如果给定键不是任何其他单词的前缀
        if (isEmpty(root)) {
            delete (root); // 删除节点
            root = NULL;
        }
        return root;
    }

    // 如果不是最后一个字符，则递归处理通过ASCII值获取的子节点
    int index = key[depth] - 'a';
    root->children[index] = remove(root->children[index], key, depth + 1);

    // 如果根节点没有任何子节点（其唯一子节点被删除），并且不是另一个单词的结尾
    if (isEmpty(root) && root->isEndOfWord == false) {
        delete (root); // 删除节点
        root = NULL;
    }
    return root;
}

// 驱动函数
int main(){
    // 输入的键（仅使用'a'到'z'的字母且为小写）
    string keys[] = { "the", "a", "there", "answer", "any", "by", "bye", "their", "hero", "heroplane" };
    int n = sizeof(keys) / sizeof(keys[0]);
    struct TrieNode* root = getNode();
    // 构建Trie树
    for (int i = 0; i < n; i++)
        insert(root, keys[i]);
    // 搜索不同的键
    search(root, "the") ? cout << "Yes\n" : cout << "No\n";
    search(root, "these") ? cout << "Yes\n" : cout << "No\n";
    search(root, "bye") ? cout << "Yes\n" : cout << "No\n";
    remove(root, "bye");
    search(root, "bye") ? cout << "Yes\n" : cout << "No\n";
    return 0;
}

i4683

p4683

P4683

Previous Topic

Back to Lesson

Next Topic