二叉搜索树(binary search tree)
组别:入门组
难度:4
一棵二叉搜索树应该满足以下条件:
1.非空左子树的所有键值都小于其根节点的键值
2.非空右子树的所有键值都大于其根节点的键值
3.左右子树都是二叉搜索树
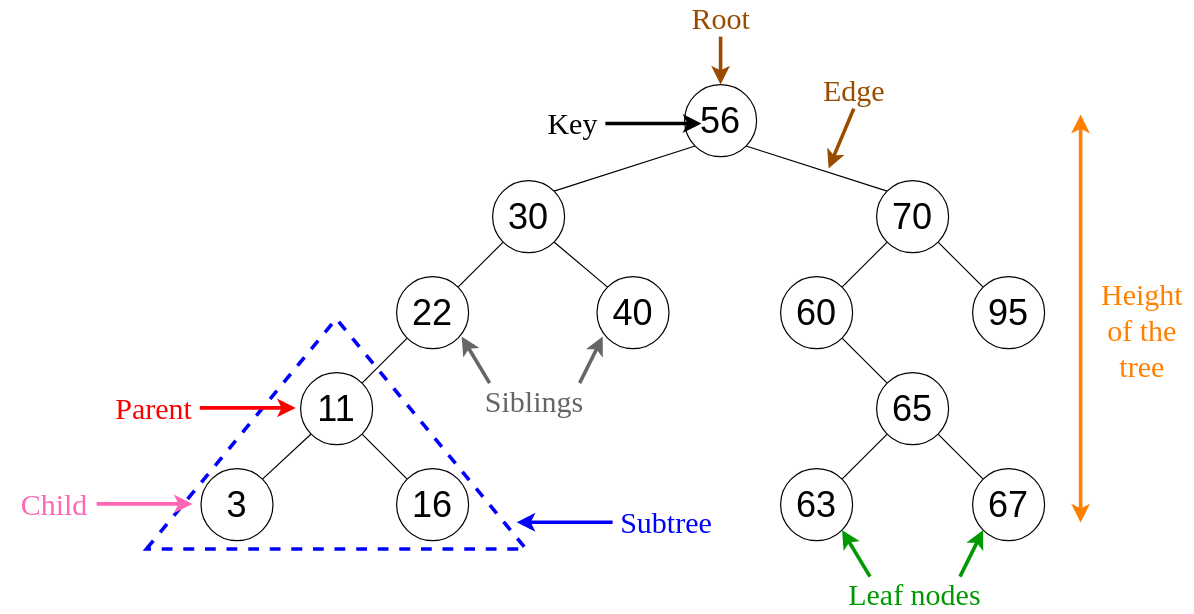
代码实现:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 | /**************************************************************** * Description: 二叉搜索树 C++ implementation of Binary Search Tree(BST) * Author: Alex Li * Date: 2023-06-10 21:10:46 * LastEditTime: 2024-08-08 10:44:11 ****************************************************************/ #include <iostream> using namespace std; struct node{ int data; struct node *left,*right; }; // 创建一个新节点 struct node* newNode(int item){ struct node *temp = new node; temp->data = item; temp->left = NULL; temp->right = NULL; return temp; } // 中序遍历 void inorder(node *root){ if(root != NULL){ // 遍历左子树 inorder(root->left); // 遍历根节点 cout << root->data << "->"; // 遍历右子树 inorder(root->right); } } // 插入节点 struct node* insertNode(node *node, int data){ // 如果树为空,返回新节点 if(node == NULL) return newNode(data); // 遍历左子树并插入节点 if(data < node->data) node->left = insertNode(node->left, data); else node->right = insertNode(node->right, data); return node; } // 找到最小值节点 struct node *minValueNode(struct node *node) { struct node *current = node; // 找到最左边的叶子节点 while (current && current->left != NULL) current = current->left; return current; } // 删除节点 struct node *deleteNode(struct node *node, int data) { // 如果树为空,返回节点 if (node == NULL) return node; // 找到要删除的节点 if (data < node->data) node->left = deleteNode(node->left, data); else if (data > node->data) node->right = deleteNode(node->right, data); else { // 如果节点只有一个子节点或没有子节点 if (node->left == NULL) { struct node *temp = node->right; delete node; return temp; } else if (node->right == NULL) { struct node *temp = node->left; delete node; return temp; } // 如果节点有两个子节点 // 找到右子树的最小值节点作为中序后继节点 struct node *temp = minValueNode(node->right); // 用中序后继节点替换要删除的节点 node->data = temp->data; // 删除中序后继节点 node->right = deleteNode(node->right, temp->data); } return node; } int main(){ struct node *root = NULL; root = insertNode(root, 8); root = insertNode(root, 3); root = insertNode(root, 1); root = insertNode(root, 6); root = insertNode(root, 7); root = insertNode(root, 10); root = insertNode(root, 14); root = insertNode(root, 4); cout << "Inorder traversal: "; inorder(root); root = deleteNode(root, 10); cout << "\nAfter deleting 10\n"; inorder(root); } |
题目:判断二叉搜索树 A1527
二叉搜索树 (BST) 递归定义为具有以下属性的二叉树:
- 若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值
- 若它的右子树不空,则右子树上所有结点的值均大于或等于它的根结点的值
- 它的左、右子树也分别为二叉搜索树
我们将二叉搜索树镜面翻转得到的树称为二叉搜索树的镜像,其中某结点大于其右侧结点,小于左则结点。中序是递减。
现在,给定一个整数序列,请你判断它是否可能是某个二叉搜索树或其镜像进行前序遍历的结果。
输入格式
第一行包含整数 N,表示节点数量。
第二行包含 N个整数。
输出格式
如果给定整数序列是某个二叉搜索树或其镜像的前序遍历序列,则在第一行输出 YES,否则输出 NO。
如果你的答案是 YES,则还需要在第二行输出这棵树的后序遍历序列。
数据范围
1≤N≤1000
输入样例1:
7
8 6 5 7 10 9 11
输出样例1:
YES
5 7 6 9 11 10 8
输入样例2:
7
8 10 11 9 6 7 5
输出样例2:
YES
11 9 10 7 5 6 8输入样例3:
7
8 6 7 5 10 9 11输出样例3:
NOQuizzes