图的基本概念

图的定义:

　　图在数据结构中是中多对多的关系，一般分为无向图与有向图
　　常用邻接矩阵或者邻接链表来表示图中结点的关系
　　⑴图是由顶点集V和顶点间的关系集合E（边的集合）组成的一种数据结构
　　⑵用二元组定义为：G=（V,E）。

A Graph is a non-linear data structure consisting of vertices and edges. The vertices are sometimes also referred to as nodes and the edges are lines or arcs that connect any two nodes in the graph. More formally a Graph is composed of a set of vertices( V ) and a set of edges( E ). The graph is denoted by G(E, V).

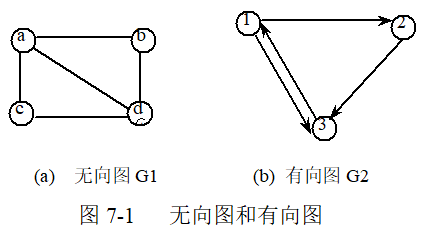
对于图7-1所示的无向图G1和有向图G2，它们的数据结构可以描述为：
　　　　　　G1=(V1,E1)， 其中 V1={a,b,c,d},E1={(a,b),(a,c),(a,d),(b,d),(c,d)},
       　　        G2=(V2,E2)，其中 V2={1,2,3}, E2={<1,2>,<1,3>,<2,3>,<3,1>}。

---

有向图与无向图

　　　　⑴在图中，若用箭头标明了边是有方向性的，则称这样的图为有向图，否则称为无向图。

　　　　如图7-1中:
   　　　　　　①G1为无向图，   ②G2 为有向图。
　　　　⑵在无向图中:一条边（x,y）与（y,x）表示的结果相同，用圆括号表示，
　　　　⑶在有向图中:一条边<x,y>与<y,x>表示的结果不相同，故用尖括号表示。<x,y>表示从顶点x发向顶点y的边，x为始点，y为终点。
　　　　⑷有向边也称为弧，x为弧尾，y为弧头,则<x,y>表示为一条弧, 而<y,x>表示y为弧尾，x为弧头的另一条弧 。

---

完全图/稠密图/稀疏图：

　　⑴具有n个顶点，n(n-1)/2条边的图，称为完全无向图，
　　⑵具有n个顶点，n(n-1) 条弧的有向图,称为完全有向图。
　　⑶完全无向图和完全有向图都称为完全图。
　　⑷对于一般无向图，顶点数为n，边数为e，则 0≤e  ≤n(n-1)/2。
　　⑸对于一般有向图，顶点数为n，弧数为e， 则 0≤e≤n(n-1)  。
　　⑹当一个图接近完全图时，则称它为稠密图，
　　⑺当一个图中含有较少的边或弧时，则称它为稀疏图。

---

度(出度/入度)：

　　⑴在图中，一个顶点依附的边或弧的数目，称为该顶点的度。
　　⑵在有向图中，一个顶点依附的弧头数目，称为该顶点的入度。
　　⑶一个顶点依附的弧尾数目，称为该顶点的出度，某个顶点的入度和出度之和称为该顶点的度。
　　⑷若图中有n个顶点，e条边或弧，第i个顶点的度为di，则有  e=1/2 * Σ(1<= i <= n,   di)

---

子图

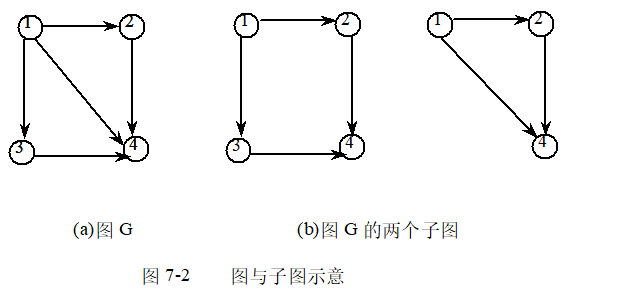
⑴若有两个图G1和G2， G1=(V1,E1)， G2=(V2,E2)， 满足如下条件：
    V2⊆V1  ，E2⊆ E1，即V2为V1的子集，E2为E1的子集，则 称图G2为图G1的子图。

---

权：

⑴在图的边或弧中给出相关的数，称为权。
⑵权可以代表一个顶点到另一个顶点的距离，耗费等，带权图一般称为网。

---

强连通图、单向连通图和弱连通图：

强连通：有向图（前提）中，任意两点都有至少一条通路，则此图为强连通图。

单向连通：有向图中，任意结点对中，至少从一个到另一个是可达的，就是单向连通。

弱连通图：将有向图的有向边换成无向边得到的图是连通图，则此有向图是弱连通图。

---

欧拉回路：

如果图G中的一个路径包括每个边恰好一次，则该路径称为欧拉路径(Euler path)。如果一个回路是欧拉路径，则称为欧拉回路(Euler circuit)。 ^[1] 具有欧拉回路的图称为欧拉图（简称E图）。具有欧拉路径但不具有欧拉回路的图称为半欧拉图。