拓扑排序(Topological svorting)
对一个有向无环图 ( Directed Acyclic Graph 简称 DAG ) G 进行拓扑排序,是将 G中所有顶点排成一个线性序列,使得图中任意一对顶点 u 和 v ,若边 < u , v > ∈ E ( G ),则 u 在线性序列中出现在 v之前。通常,这样的线性序列称为满足拓扑次序 ( Topological Order )
的序列,简称拓扑序列。简单的说,由某个集合上的一个偏序得到该集合上的一个全序,这个操作称之为拓扑排序。
拓扑排序是存在在DAG中,而在DAG中因为是无环的,所以必然存在一个点v1他是入度为0的,那么这个入度为0的点就是当前的出发点。注意:拓扑排序有时结果不唯一。
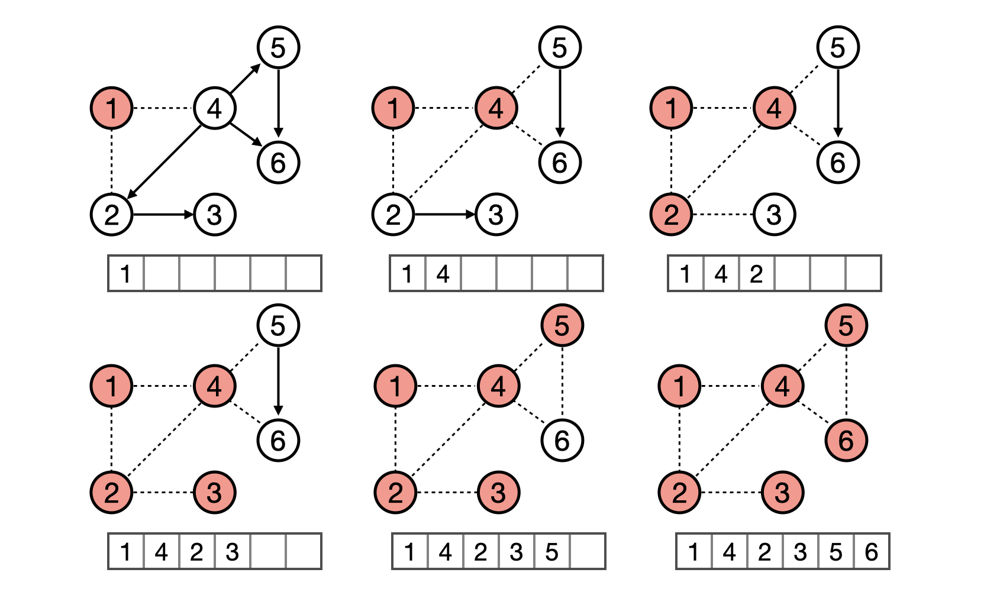
1.找一个入度为零的端点,如果有多个,则从编号小的开始找;
2.将该端点的编号输出;
3.将该端点删除,同时将所有由该点出发的有向边删除;
4.循环进行 1,2 和 3 ,直到图中的图中所有点的入度都为零;
5.拓扑排序结束;
代码实现:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 | /**************************************************************** * Description: topoSort * Author: Alex Li * Date: 2023-06-30 21:49:30 * LastEditTime: 2024-01-29 23:15:02 ****************************************************************/ #include <iostream> #include <vector> #include <queue> using namespace std; int n,m; const int N=1000; vector<int> e[N],tp; //e[x]存点x的邻点,tp存拓扑序列; int din[N]; //存结点的入度 bool TopoSort(){ queue<int> q; for (int i =1; i <=n; i++){ if(din[i]==0) q.push(i);//将入度为0的结点入到q队列里。 } while(q.size()){ int x=q.front(); //把q队列首元素赋值给x q.pop(); //首元素出q队列 tp.push_back(x); //入到tp序列 for (int i = 0; i < e[x].size(); i++){ ////将刚出列x结点所有相联的结点的入度减1,如果入度是0,就入到q队列里 if(--din[e[x][i]]==0)q.push(e[x][i]); // for (auto y:e[x]) if(--din[y]==0)q.push(y); } } return tp.size()==n; //如果拓扑序列个数和元素个数一样,说明可以拓扑排序 } int main(){ int a,b; //n是指结点数,m是边数 cin>>n>>m; for (int i = 0; i < m; i++){ cin>>a>>b; e[a].push_back(b); din[b]++; //记录没个节点的入度 } if(!TopoSort()) puts("TopoSort is not supported"); else for (int i = 0; i <n; i++)cout<<tp[i]; return 0; } |
测试数据:
6 7
1 2
1 4
2 3
4 2
4 6
4 5
5 6
输出:142536
练习:P3644
Quizzes